Sterowanie robotem Astorino po kuli

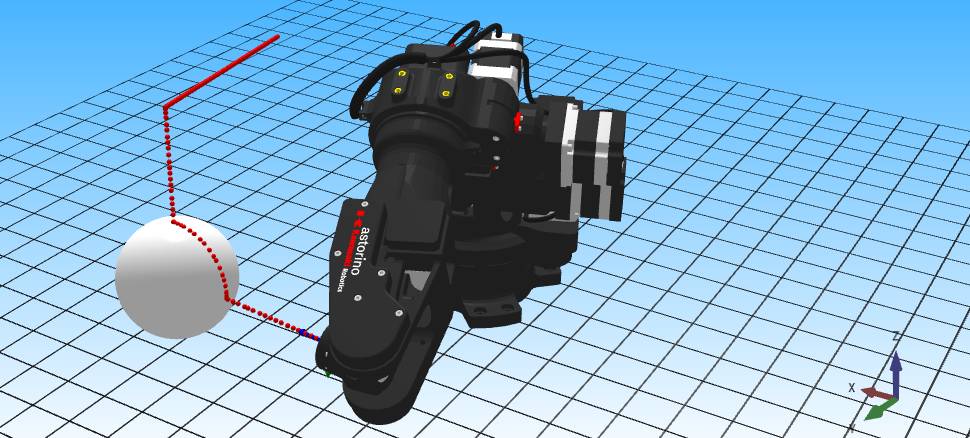
Dzięki temu poradnikowi dowiesz się, jak zasymulować ruch robota Astorino po powierzchni kuli przy pomocy astorinoIDE, a następnie zaimplementować i przetestować program sterowania w rzeczywistych warunkach. Zaczniemy od matematycznego opisu trajektorii ruchu robota, a następnie stworzymy kod w Pythonie, który obliczy położenie i orientację na powierzchni kuli. W końcu przeniesiemy program do astorinoIDE i przetestujemy go na robocie edukacyjnym Astorino, sprawdzając poprawność wykonania ruchu.

Potrzebne urządzenia oraz oprogramowanie

• Robot Astorino wraz z oprogramowaniem.
• Oprogramowanie astorinoIDE.
• ASTORINO-OPT-SIMBOX (do testowania symulacji).
• Środowisko programistyczne Python (wraz z biblioteką NumPy).
• Komputer PC z systemem operacyjnym Windows.

Wstęp

Poruszanie robotem w przestrzeni trójwymiarowej stanowi wyzwanie, szczególnie gdy wymagana jest precyzyjna nawigacja po powierzchni sferycznej. Roboty muszą radzić sobie z realizacją skomplikowanych trajektorii, które mogą obejmować zarówno ruchy po prostych, jak i bardziej złożonych powierzchniach, takich jak kula.

W artykule przedstawiono dwie metody sterowania robotem Astorino, umożliwiające realizację ruchu po powierzchni kuli. Pierwsza z nich opiera się na przesunięciu punktu TCP (Tool Center Point) do środka kuli, podczas gdy druga metoda wykorzystuje matematyczny opis kuli oraz odpowiednią transformację układu współrzędnych. W dalszej części artykułu przedstawiono szczegóły implementacji tych metod w oprogramowaniu astorinoIDE oraz sposób generowania trajektorii robota.

Sterowanie ruchem po kuli na podstawie punktu TCP

Pierwsza metoda sterowania po kuli polega na przesunięciu punktu TCP do środka kuli. Aby to osiągnąć, należy najpierw oddalić układ narzędzia (TOOL) od końcówki robota (narzędzia lub flanszy), a następnie dojechać robotem w taki sposób, aby punkt TCP pokrył się z centrum kuli. Po wykonaniu tego ruchu, rotacja robota względem osi X i Y układu TOOL zapewnia ruch robota po powierzchni kuli. Tego rodzaju sterowanie jest stosunkowo proste, ale może wymagać dużej precyzji w ustawieniach początkowych układu.

Sterowanie na podstawie opisu matematycznego kuli

Wielkości służące do opisu położenia na powierzchni kuli

Alternatywnym podejściem do poruszania robotem po kuli jest wykorzystanie jej matematycznego opisu w przestrzeni trójwymiarowej. Można to zrobić poprzez określenie odpowiednich parametrów kuli i obliczenie pozycji oraz orientacji punktów na jej powierzchni. Będziemy używali oznaczeń:

• S(x₀,y₀,z₀) – środek kuli,
• P(x,y,z) – dowolny punkt na powierzchni kuli,
• R_k – promień kuli
• θ – kąt zenitalny
• Φ – azymut

Kąt zenitalny to kąt między osią globalnego pionu (osią Z) a wektorem prowadzącym od środka kuli do punktu na jej powierzchni. Kąt ten jest dodatni, gdy mierzony jest od osi Z w kierunku promienia prowadzącego do danego punktu na kuli.

Azymut to kąt między osią X a rzutem wektora prowadzącego od środka kuli do punktu na jej powierzchni na płaszczyznę poziomą XY. Kąt ten jest dodatni, gdy mierzony jest od osi X w kierunku osi Y.

Powyższe definicje kątów zostały zobrazowane poniżej (rys. 1).

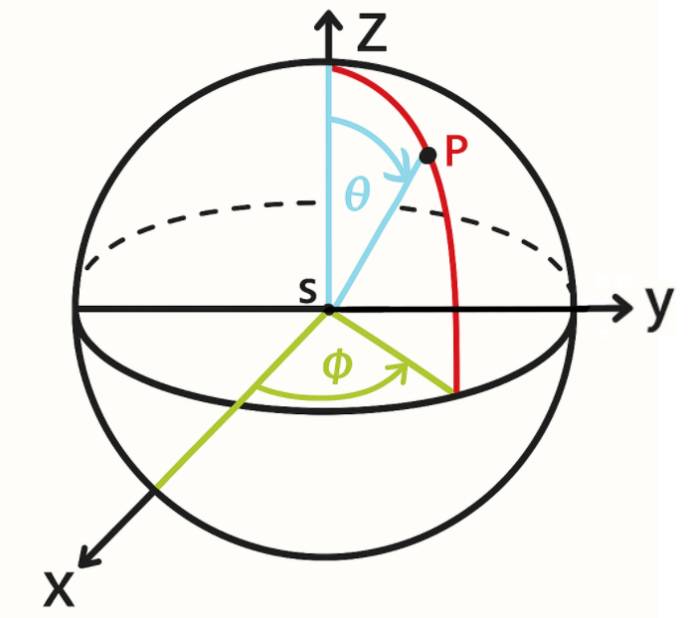
Na przykładzie kuli ziemskiej:

• kąt zenitalny – określa szerokość geograficzną,
• azymut – określa długość geograficzną.

Matematyczny opis położenia i orientacji na kuli

Wykorzystując powyższe oznaczenia można zapisać wzory na współrzędne położenia na powierzchni kuli:

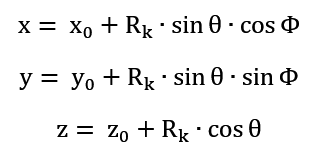
Wyznaczenie orientacji narzędzia należy przeprowadzić w taki sposób, aby oś Z układu TOOL była skierowana prostopadle do powierzchni kuli, a jej przedłużenie przechodziło przez środek kuli.

 Na początek należy określić oś Z narzędzia jako:

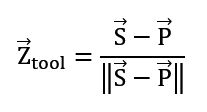
Jest to znormalizowany wektor wskazujący w stronę środka kuli.

Następnie konieczne będzie wyznaczenie osi X. Zostanie ona określona jako styczna do powierzchni kuli, wyznaczona na podstawie pochodnej położenia względem kąta zenitalnego. Jeśli kąt zenitalny jest stały (co skutkuje zerową pochodną), oś X będzie wyznaczona jako pochodna położenia względem kąta azymutu. W celu obliczenia tej orientacji skorzystano ze wzorów:

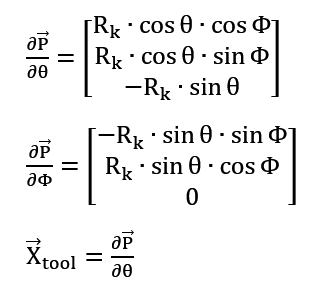
Jeśli jednak pochodna jest bliska zeru, to przyjmujemy kierunek osi X jako:

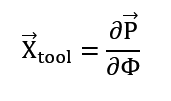
Oś Y musi dopełniać utworzony układ prawoskrętny:

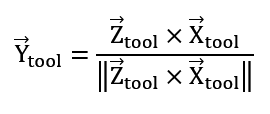
W ostatnim kroku należy jeszcze raz wyznaczyć kierunek osi X, aby zapewnić ortonormalność układu współrzędnych narzędzia.

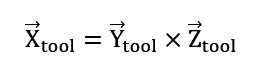
Mając wektory:

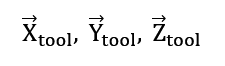
budujemy macierz rotacji:

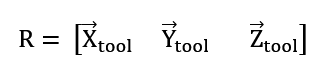
Na jej podstawie możemy wyznaczyć kąty Eulera (w konwencji ZYZ), które jednoznacznie opisują orientację narzędzia w przestrzeni 3D.

Implementacja sterowania w programie astorinoIDE

Na początek włączamy program astorinoIDE. Wybieramy rodzaj połączenia z listy rozwijanej (w przykładzie wybrano połączenie USB) oraz klikamy przycisk Connect/Disconnect (rys.2).

Wybieramy kierunek przesyłanych danych z komputera do robota oraz klikamy SYNC (rys. 3).

W kolejnym kroku otwieramy lub tworzymy nowy projekt z górnego paska. W tym celu klikamy Project i wybieramy odpowiednią opcję z listy rozwijanej (rys. 4).

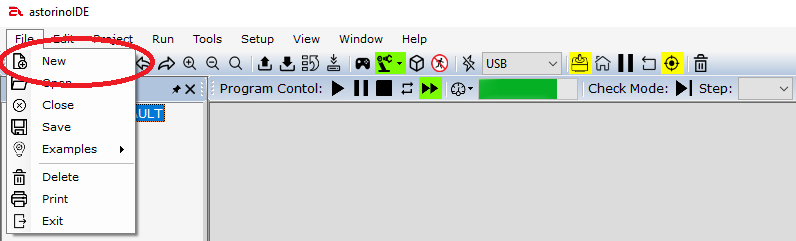
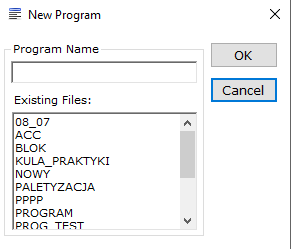
Następnie otwieramy lub tworzymy nowy program. Z lewego drzewa folderów możemy wybrać istniejący plik z zakładki Program Files lub utworzyć nowy program za pomocą opcji w górnym pasku i zakładce File. Po wybraniu nowego programu (rys. 5) wyświetli się okno, w którym wpisujemy nazwę pliku i zatwierdzamy przyciskiem OK (rys. 6).

Po połączeniu z robotem i stworzeniu własnego programu można zacząć tworzyć scenę (układ robota z kulą w przestrzeni). W celu otwarcia symulacji należy kliknąć przycisk Visualization (rys. 7), oznaczony na pasku głównym programu symbolem sześcianu.

Po kliknięciu powinno pojawić się okno z robotem (rys. 8).

W celu ułatwienia sterowania robotem możemy sprowadzić go do pozycji domowej. Jest to procedura, która umożliwia szybkie przywrócenie robota do wyjściowej pozycji, co ułatwia dalsze programowanie i wykonywanie poleceń. W tym celu w terminalu w dolnej części programu astorinoIDE (rys. 9) wpisujemy komendę do home i zatwierdzamy wciskając Enter na klawiaturze.

Po takim wywołaniu komendy terminal powinien odpowiedzieć tekstem „DO motion Completed” (rys.10), a robot powinien znaleźć się w pozycji domowej (rys. 11).

UWAGA! Należy pamiętać, że aby ruch został wykonany, robot musi znajdować się w trybie Repeat Mode. Zmienić go można w górnym pasku narzędzi: Mode -> Switch to Repeat (ikona robota) (rys. 12).

Gdy mamy już otwarty projekt z naszym programem oraz okno symulacji, możemy dodać przykładową kulę, po której później będzie poruszał się robot. W tym celu w oknie wizualizacji wybieramy opcję Open Shape Generator (rys. 13).

Otworzy nam się po prawej stronie symulacji okno tworzenia wybranego kształtu w przestrzeni. W celu dodania kuli wybieramy zakładkę Sphere (rys. 14). Następnie możemy wprowadzić jej parametry: nazwę, promień, położenie w trzech osiach układu globalnego, kolor oraz rodzaj obiektu:

• Obstacle – obiekty tego typu są statycznymi obiektami sceny,
• Work – obiekty tego typu mogą być przenoszone przez robota,
• Tool – obiekty tego typu zawsze poruszają się zgodnie z kiścią robota. 

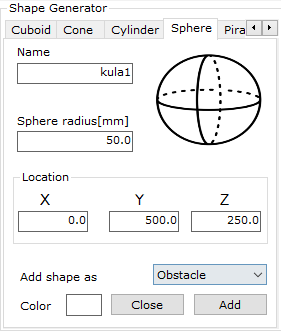
Gdy wszystkie parametry zostały już ustawione, należy kliknąć przycisk Add.

Ruch po kuli przez rotację wokół oddalonego punktu TCP

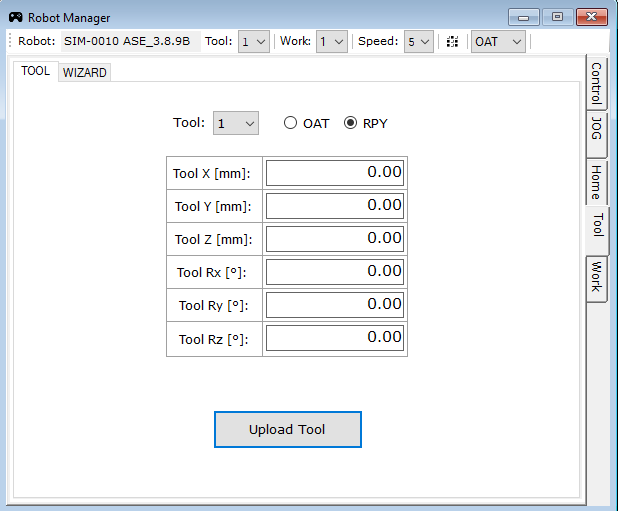
Pierwszym sposobem na ruch po kuli jest oddalenie punktu TCP na odległość równą jej promieniowi. W tym celu otwieramy okno Robot Manager (rys. 15).

Po pojawieniu się okna należy wejść w zakładkę TOOL z prawej strony (rys. 16) i jako parametr TOOL Z, wpisać wartość wcześniej ustawionego promienia kuli.

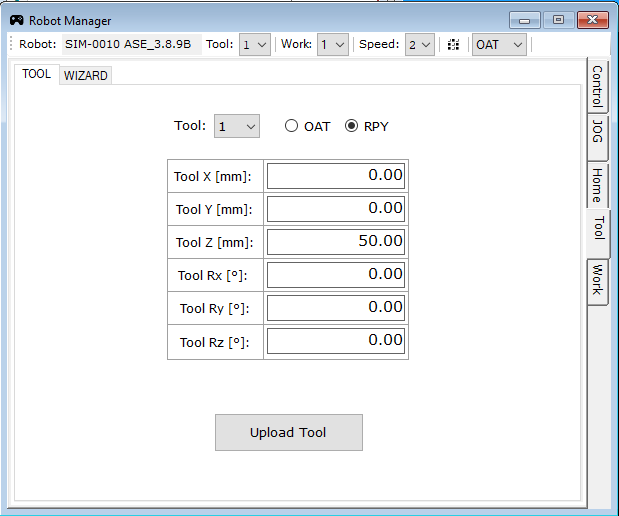
Klikamy Upload Tool oraz zatwierdzamy zmianę narzędzia po wyświetleniu ostrzeżenia.

W kolejnym kroku dojeżdżamy do kuli, tak by punkt TCP pokrył się z środkiem kuli, a orientacja narzędzia była prostopadła do powierzchni kuli. Wykorzystać do tego możemy zakładkę JOG w oknie Robot Manager (rys. 17). Wybieramy układ, w którym chcemy poruszyć robotem z listy rozwijanej (Jogging -> Mode) i klikając odpowiednie przyciski dojeżdżamy nim do wcześniej wspomnianej pozycji (rys.18). Jest to możliwe dopiero po zmianie trybu pracy na Teach Mode.

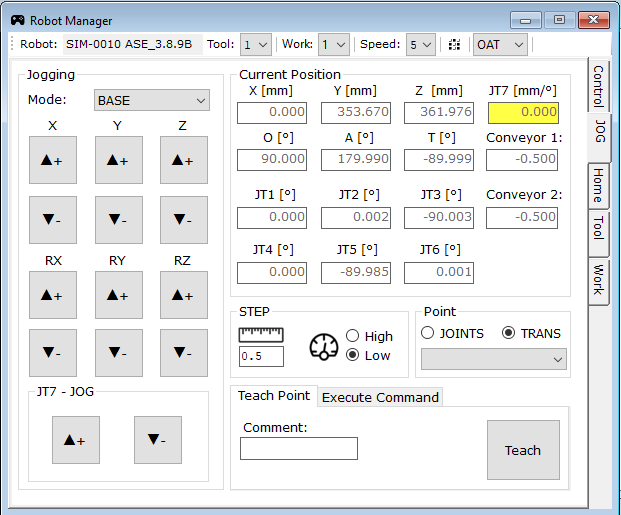
Następnie możemy już poruszać po kuli. W tym celu wybierany w zakładce JOG ruch robotem w układzie TOOL i wykonujemy rotację wokół osi X oraz Y (rotacja wokół osi Z nie ma sensu, ponieważ wcześniej skierowaliśmy ją prostopadle do powierzchni kuli). Poniżej przedstawiono kilka przykładowych pozycji robota.

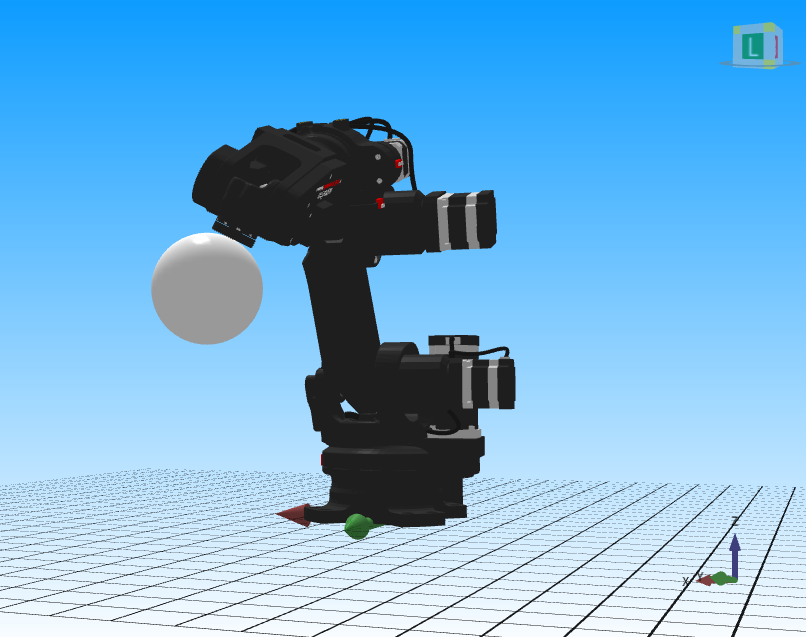
Ruch po kuli przez wykorzystanie jej matematycznego opisu

Drugą metodą na poruszaniem robotem po kuli jest wygenerowanie punktów (położenie i orientacja), zgodnie z opisem zamieszczonym we wcześniejszej części artykułu. Napisano do tego celu program w języku Python, który generuje punkty na powierzchni kuli wraz z orientacją układu TOOL..

Uwaga! Jeśli położenie lub orientacja układu TOOL zostały zmienione, tak jak chociażby w poprzednim paragrafie, należy przywrócić układ do ustawień podstawowych (zerując każdą ze składowych położenia i orientacji – rys. 22).

Uniwersalność opracowanego kodu pozwala na wyznaczanie położenia oraz orientacji układu narzędzia w przestrzeni kulistej, niezależnie od położenia kuli oraz jej promienia. Dzięki temu możliwe jest obliczenie współrzędnych punktów na powierzchni kuli w różnych konfiguracjach.

Warto jednak zauważyć, że program nie uwzględnia rzeczywistych ograniczeń robota, takich jak fizyczne możliwości jego ruchu, zasięg czy przechyły. W praktyce oznacza to, że wskazane przez program punkty mogą nie zawsze być osiągalne przez robota w rzeczywistych warunkach. Program dostarcza jedynie wyników matematycznych, które odnoszą się do idealnego modelu matematycznego kuli, nie biorąc pod uwagę fizycznych ograniczeń robota, takich jak kinematyka, zasięg, czy ograniczenia mechaniczne.

Istnieje zatem potrzeba dalszej weryfikacji wyników w kontekście realnych trajektorii robota dla konkretnego zastosowania. W artykule skupiono się jednak na implementacji samego ruchu, a nie na konkretnych zastosowaniach.

Aby ułatwić implementację kodu oraz uniknąć nadmiaru złożonych nazw, w kodzie zastosowane zostały następujące oznaczenia:

• kąt zenitalny: θ = u
• azymut: Φ = v

Poniżej przedstawiony został kod w języku Python, który pozwala na generowanie wybranej liczby punktów na powierzchni kuli o dowolnych – wybranych wcześniej – parametrach.

import numpy as np
from scipy.spatial.transform import Rotation as R

# Parametry kuli
x0, y0, z0 = 0.0, 500.0, 250.0  # środek kuli
R_kuli = 50.0  # promień
N = 20  # liczba punktów

for i in range(N):
    u = i * np.pi / (N - 1)  # kąt zenitalny
    v = np.pi  # azymut

    # Pozycja na powierzchni kuli
    x = x0 + R_kuli * np.sin(u) * np.cos(v)
    y = y0 + R_kuli * np.sin(u) * np.sin(v)
    z = z0 + R_kuli * np.cos(u)
    position = np.array([x, y, z])
    center = np.array([x0, y0, z0])

    # Oś Z narzędzia (do środka kuli)
    Z_tool = center - position
    Z_tool /= np.linalg.norm(Z_tool)

    # Dwa wektory styczne do powierzchni (pochodne po u i v)
    dP_du = np.array([
        R_kuli * np.cos(u) * np.cos(v),
        R_kuli * np.cos(u) * np.sin(v),
        -R_kuli * np.sin(u)
    ])
    dP_dv = np.array([
        -R_kuli * np.sin(u) * np.sin(v),
        R_kuli * np.sin(u) * np.cos(v),
        0.0
    ])

    # Wybierz jeden z wektorów stycznych (np. dP_dv)
    tangent = dP_dv
    if np.linalg.norm(tangent) < 1e-6:  # zabezpieczenie przed zerowym wektorem
        tangent = dP_du
    tangent /= np.linalg.norm(tangent)

    # Budowa układu współrzędnych
    X_tool = tangent
    Y_tool = np.cross(Z_tool, X_tool)
    Y_tool /= np.linalg.norm(Y_tool)
    X_tool = np.cross(Y_tool, Z_tool)
    X_tool /= np.linalg.norm(X_tool)

    # Macierz rotacji i konwersja do kątów Eulera
    R_matrix = np.column_stack((X_tool, Y_tool, Z_tool))
    rot = R.from_matrix(R_matrix)
    euler_deg = rot.as_euler('zyz', degrees=True)

    # Format wyjścia: x,y,z,roll,pitch,yaw
    print(f"{x:.3f},{y:.3f},{z:.3f},{euler_deg[2]:.3f},{euler_deg[1]:.3f},{euler_deg[0]:.3f}")

Program służy do wyznaczenia pozycji i orientacji zestawu punktów znajdujących się na powierzchni kuli. Na początku definiowane są podstawowe parametry kuli: jej środek w przestrzeni trójwymiarowej, promień oraz liczba punktów, które mają zostać rozmieszczone na powierzchni.

Następnie, w pętli, dla każdego z tych punktów wyliczana jest jego dokładna pozycja na kuli, przy czym zmieniany jest tylko kąt zenitalny, a azymut pozostaje stały. Dzięki temu punkty są rozmieszczone wzdłuż jednego południka. Dla każdego punktu na powierzchni kuli wyznaczany jest wektor skierowany od tego punktu do środka kuli. Ten wektor określa kierunek, w którym „patrzy” narzędzie lub układ współrzędnych przypisany do punktu – jest to oś Z lokalnego układu.

Aby określić pełną orientację w przestrzeni, potrzebne są jeszcze osie X i Y. Do tego wykorzystywane są dwa wektory styczne do powierzchni kuli, obliczane jako pochodne pozycji punktu względem kątów sferycznych. Jeden z tych wektorów jest wybierany jako podstawa do określenia osi X, a jeśli jego długość byłaby zbyt mała, wybierany jest drugi. Wektor ten jest następnie normalizowany, czyli przeliczany tak, aby miał długość równą 1.

Dalej budowany jest ortogonalny układ współrzędnych. Oś Y wyznaczana jest jako wektor prostopadły do osi Z i wybranego wektora stycznego, a następnie ponownie wyznaczana jest oś X, by zagwarantować, że wszystkie trzy osie tworzą spójny, prawidłowy układ. Z tych trzech wektorów tworzona jest macierz rotacji, która opisuje, jak lokalny układ współrzędnych punktu jest ustawiony względem układu globalnego. Na koniec z tej macierzy wyciągane są kąty Eulera, które opisują orientację punktu jako sekwencję obrotów wokół osi. Wypisywana jest pozycja punktu oraz te trzy kąty, co razem stanowi pełną informację o położeniu i ustawieniu w przestrzeni.

Aby zweryfikować poprawność generowanych punktów, opracowano prosty program w astorinoIDE, który wykorzystuje trzy z wcześniej obliczonych punktów na powierzchni kuli. Program ten wykonuje ruch robota po łuku, w którym pierwszy punkt pełni rolę punktu początkowego, drugi – punktu pomocniczego, a trzeci – punktu końcowego. Dzięki tej metodzie można wizualnie sprawdzić, czy robot prawidłowo podąża wyznaczoną trajektorią. Poniżej przedstawiono kod programu realizującego ten ruch:

.PROGRAM KULA
  HOME
  lappro P1, 100
  lmove P1
  c1move P2
  c2move P3
  ldepart 100
.END

Do przeniesienia obliczonych punktów do programu w astorinoIDE wystarczy skopiować wybrane punkty, które zostały zwrócone w wyniku kompilacji programu w Pythonie. Po wygenerowaniu punktów, należy je ręcznie wprowadzić do środowiska robota, co umożliwia ich dalsze wykorzystanie w kolejnych etapach aplikacji. Poniżej przedstawiono przykładowe wyniki uzyskane po kompilacji kodu (rys. 23).

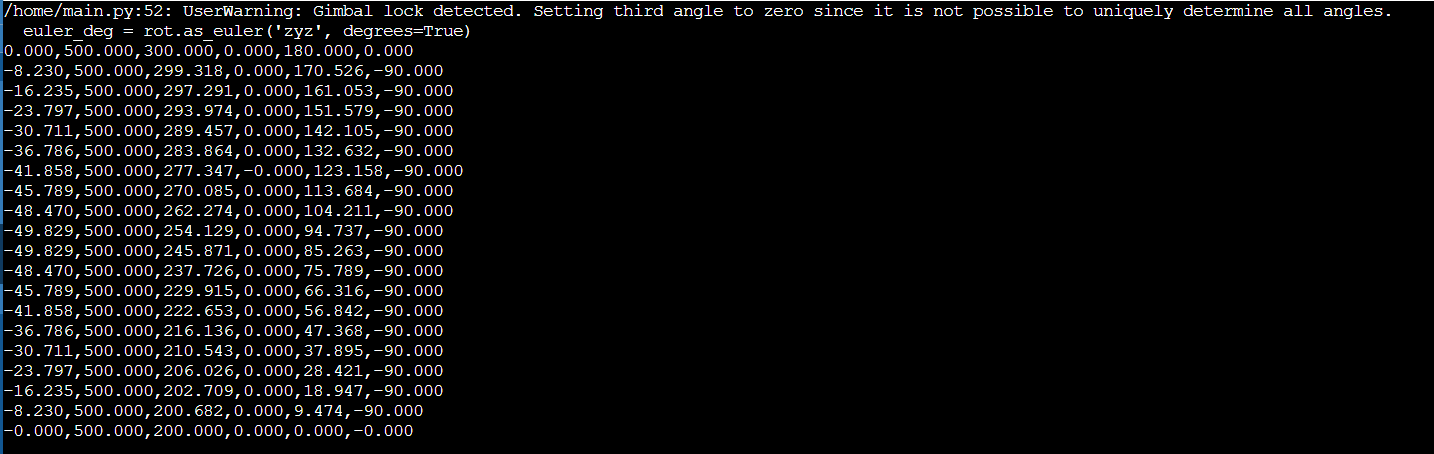
Warto tu zwrócić uwagę na ostrzeżenie, które informuje, że wykryto tzw. „gimbal lock” przy konwersji rotacji na kąty Eulera w układzie 'zyz’, co oznacza, że jedna z osi obrotu pokrywa się z inną, przez co jeden z kątów (trzeci) nie może być jednoznacznie określony i zostaje ustawiony na zero.

Jeśli chcemy przenieść pierwszy punkt do astorinoIDE, wystarczy wykorzystać w terminalu (rys. 24) polecenie POINT oraz TRANS.

Po zatwierdzeniu klawiszem Enter punkt zostanie zapisany. Jeśli chcielibyśmy sprawdzić, czy rzeczywiście tak się stało, należy wejść w zakładkę Points -> Transformation. Wyświetli się wówczas okno z zapisanymi punktami (rys. 25), wśród których powinniśmy dostrzec nasz zapisany punkt, tak jak poniżej:

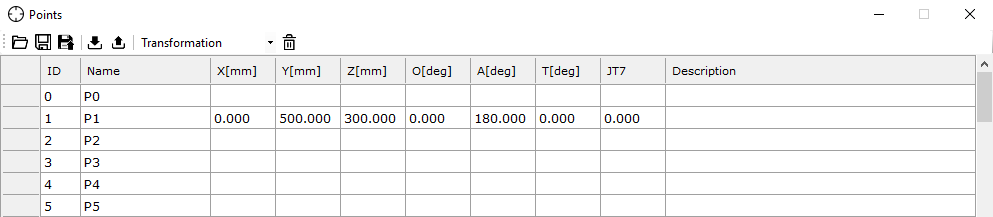
Proces ten należy powtórzyć dla dwóch pozostałych punktów. Ważne jest, aby każdy z tych punktów został zadeklarowany pod innym numerem porządkowym, np. p2, p3, itd., aby zachować spójność w dalszej części programu i umożliwić prawidłowe przypisanie do odpowiednich pozycji w przestrzeni robota.

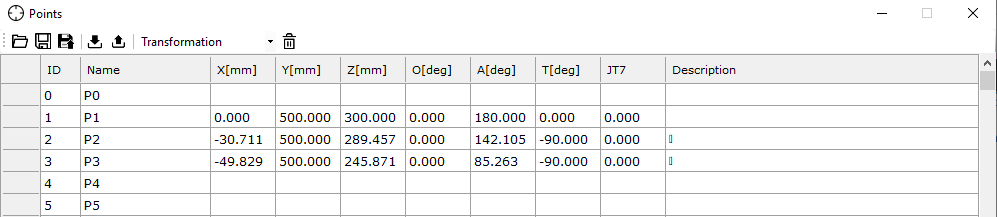
W celu przetestowania programu należy rozpocząć cykl, klikając przycisk Cycle Start.

Jeśli chcemy uruchomić program od początku lub od jakiegoś konkretnego kroku (który nie jest pierwszym), należy wcisnąć kolejno Pause oraz Cycle Stop. Następnie z listy rozwijanej Step należy wybrać linijkę kodu, od której chcemy zacząć wykonywanie ruchu. Rozpoczęcie ruchu zaczynamy kliknięciem przycisku Pause, a następnie przyciskiem Cycle Start.

Wynik programu przedstawiono na rysunku poniżej:

Z analizy wynika, że wartość azymutu pozostaje stała (rys. 29), podczas gdy kąt zenitalny zmienia się w zakresie od 0do około 90, przy czym ostatni punkt charakteryzuje się właśnie takim kątem. Ruch odbywa się wyłącznie w płaszczyźnie XZ (dla y = const. = y₀).

Program przetestowano również dla innych wartości kąta zenitalnego i azymutu. Tym razem przyjęto następujące wartości konta zenitalnego θ i azymutu Φ:

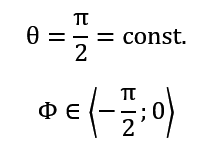
Wartość azymutu będzie zmieniała się w pętli zgodnie z następującym wzorem:

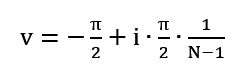
Odpowiadająca temu linijka kodu w Pythonie to:

v = -np.pi / 2 + i * (np.pi / 2) / (N - 1))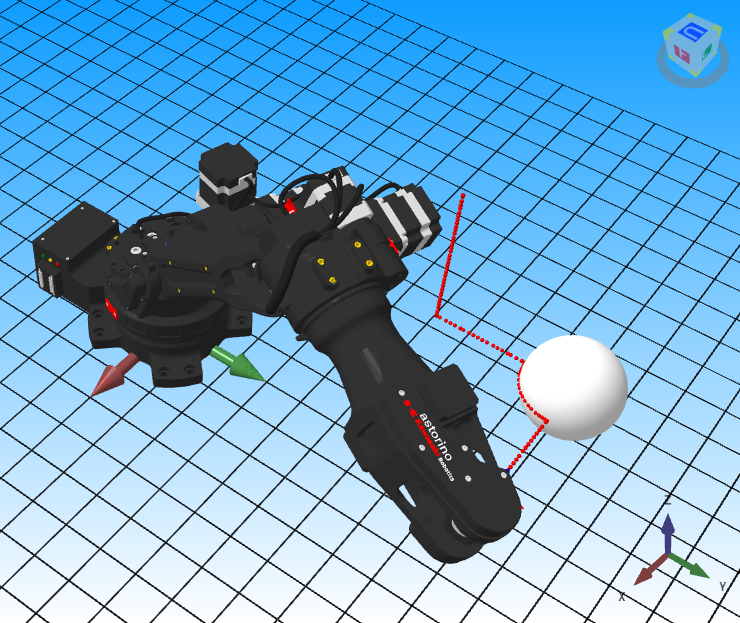

W tym przypadku (rys. 30) kąt zenitalny pozostaje stały, co powoduje, że ruch odbywa się w płaszczyźnie XY (dla z = const. = z₀).

Poniżej przedstawiono dwie inne wygenerowane trajektorie:

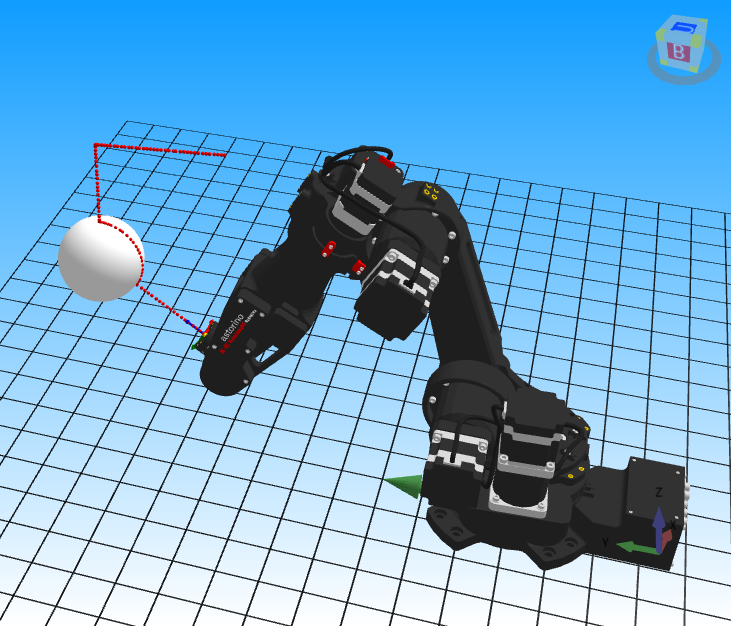
W tym artykule zaprezentowano dwie metody sterowania robotem Astorino po powierzchni kuli, z których każda ma swoje zalety i ograniczenia. Pierwsza metoda jest prostsza i bardziej intuicyjna, opiera się na prostych obliczeniach geometrycznych. Druga metoda, choć bardziej skomplikowana, pozwala na większą elastyczność i precyzję, ponieważ umożliwia generowanie punktów i orientacji narzędzia na podstawie matematycznego opisu kuli.

Praktyczna realizacja sterowania w oprogramowaniu astorinoIDE pozwala na symulację ruchów robota, co jest niezbędne do testowania poprawności trajektorii przed ich rzeczywistym wykonaniem. Zarówno metody sterowania, jak i implementacja w astorinoIDE stanowią solidną podstawę do dalszego rozwoju technologii sterowania robotem Astorino po powierzchniach sferycznych. W przyszłości można je dostosować do bardziej zaawansowanych aplikacji, wymagających precyzyjnego ruchu po bardziej złożonych trajektoriach, czy nawet w przestrzeniach o bardziej złożonych kształtach.