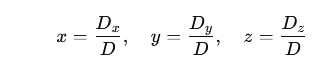Wykrywanie obiektu „w locie” na robotach Kawasaki Robotics – porównanie funkcji HSENSE oraz XMOVE

W pewnym uproszczeniu można powiedzieć, że robot pracujący w aplikacji z pola szeroko rozumianego handlingu ma za zadanie przenieść przedmiot z punktu A do punktu B. Gdy wszystkie elementy znajdują się idealnie na miejscu, zadanie jest proste w realizacji i szybkie do zaprogramowania.  Jak jednak wiadomo, niezmiernie rzadko się zdarza, że wszystkie elementy znajdują się idealnie na miejscu. Do sprawnego działania elementy należy pozycjonować lub znajdować.  Jak zatem poradzić sobie w przypadku, gdy wymiary i pozycja przedmiotu mogą się różnić od zadanych?    

W takim wypadku potrzebujemy wyposażyć robota w zmysł widzenia lub dotyku, aby znaleźć i zmierzyć poszukiwany przedmiot. Można to zrobić a pomocą systemów wizyjnych 2D i 3D, które jednak mogą okazać się zbyt drogie, aby aplikacja osiągnęła akceptowalne ROI, szczególnie biorąc pod uwagę fakt, że nie wykorzystamy nawet ułamka ich potencjału.

Do detekcji obiektu wystarczą nam podstawowe czujniki różnych typów np. optyczne, pojemnościowe, indukcyjne czy inne – o właściwym dla poszukiwanego materiału typie detekcji. Jednak dają nam one informację wyłącznie o obecności przedmiotu. Jak zatem dokonać pomiarów i zorientować przedmiot w przestrzeni?

Wykorzystując informację o detekcji przedmiotu, pozycję robota, matematykę i odrobinę inżynierskiego sprytu jesteśmy w stanie znaleźć i rozpoznać wiele cech geometrycznych przedmiotu oraz jego pozycję względem robota.

Definicja problemu inżynierskiego

Niech w dalszej części towarzyszy nam następujący problem inżynierski:

Na stacji pobrania znajdują się stalowe krążki o znanej średnicy i znanej grubości. W gniazdo poboru odkładane są ręcznie . Stos detali zawsze liczy 3 sztuki i po wykorzystaniu wszystkich jest ponownie uzupełniany przez operatora. Detale pobierane są chwytakiem szczękowym. Robot wyposażony jest w czujnik optyczny. Plamka czujnika ma 2 mm średnicy. Nasz chwytak ma 7 mm luzu pomiędzy szczękami a przedmiotem przy w pełni otwartych szczękach. Błąd pozycji większy niż 7 mm będzie skutkował kolizją robota. W jaki sposób znaleźć środki okręgów poszczególnych krążków, które będą pozycjami pobrania?

Obliczenia         

Aby wyznaczyć środek okręgu, potrzebujemy przynajmniej 3 punktów na okręgu.

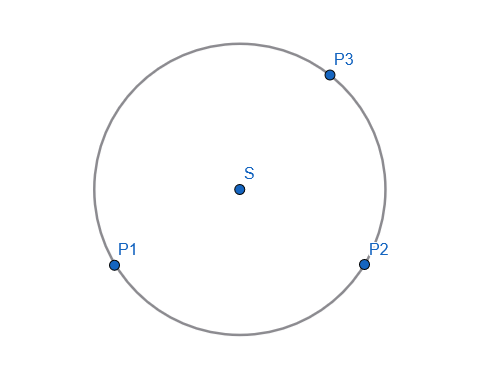
Równanie dla okręgu na płaszczyźnie

Dla okręgu znajdującego się na płaszczyźnie obliczenia wyglądają następująco:

1. Równania dla płaszczyzny:

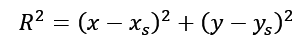
2. Do wzoru podstawiamy współrzędne 3 punktów:

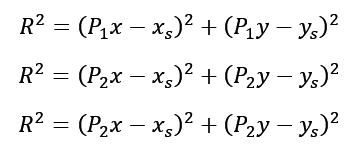
3. Na podstawie tych wzorów  układamy układ równań:

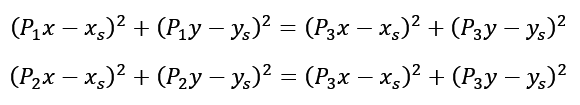
Następnie wykorzystując wzory skróconego mnożenia przekształcamy układy równań, aby z nich uzyskać wartości x_s oraz y_s , które oznaczają środek naszego poszukiwanego okręgu:

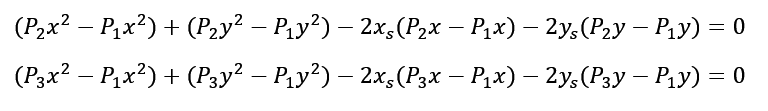
Następnie używając metody podstawienia:

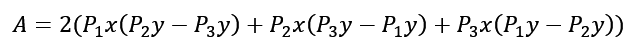
wyznaczamy współrzędne x_s oraz y_s :

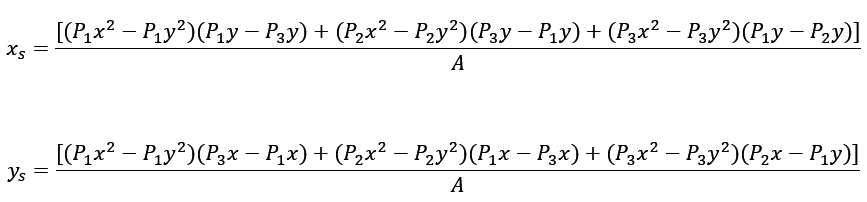
Znając współrzędne punktów na okręgu i podstawiając je do powyższych wzorów uzyskamy współrzędne środka okręgu.

Równania dla przestrzeni trójwymiarowej

Powyższe wyprowadzenie jest pewnym uproszczeniem, ponieważ robot pracuje w przestrzeni trójwymiarowej. Aby niepotrzebnie nie odchodzić od głównej treści artykułu, wyprowadzenie równań dla przestrzeni trójwymiarowej zostało przedstawione w dodatku na końcu artykułu.

Zapis obliczeń w programie robota

Obliczenia dla punktów na płaszczyźnie są już dość skomplikowane i  czasochłonne do wprowadzenia w postaci funkcji matematycznych w programie robota. Na szczęście nie musimy wprowadzać ich sami, ponieważ istnieje gotowa funkcja do wyznaczenia środka okręgu:  CCENTER.

CCENTER( pose1,pose2,pose3,pose4)

Punkty 1-3 mają znajdować się na okręgu a czwarty punkt służy do przepisania pożądanej orientacji.

Oprogramowanie problemu inżynierskiego

Część matematyczną mamy za sobą. Jak teraz znaleźć 3 punkty na krawędzi naszego przedmiotu?

Zazwyczaj programiści wykorzystują do tego funkcję XMOVE, która zezwala na ruch robota aż do pojawienia się określonego sygnału wejściowego.  Następnie następuje zatrzymanie robota i po zatrzymaniu programista zapisuje aktualną pozycję TCP jako punkt detekcji. Minusem tego rozwiązania jest potrzeba stabilnego sygnału z czujnika przez min. 50 ms, aby został uznany za detekcję, a także droga hamowania robota. Jeśli robot z ciężkim chwytakiem będzie hamował z wysokiej prędkości, to delikatnie rozminie się z pozycją wykrycia.

Przy zastosowanie programu przedstawionego poniżej, pozycja wykrycia będzie uzależniona od czasu działania i histerezy czujnika oraz prędkości TCP robota.  Im wyższa będzie prędkość robota, tym dalej od wykrytej krawędzi będzie znajdował się punkt detect1.

XMOVE pt1 TILL 1001
BREAK
HERE detect1
…

Funkcją, która w momencie detekcji przez czujnik zapisze nam pozycję robota do pamięci, jest funkcja HSENSE. Monitoruje ona stan sygnału czujnika i w przypadku zmiany jego poziomu zapisuje aktualną wartość złączową do bufora.  Do jej pracy nie jest wymagane przerwanie ruchu robota, a wymagany czas trwania sygnału nie jest tak wysoki, jak w przypadku XMOVE. Zwykle wystarcza 2 ms, ponieważ jest to czas odświeżania wejść w przypadku większości kontrolerów Kawasaki.

Jak zatem wykorzystać opisane funkcje w praktyce?

Przykład kodu z wykorzystaniem funkcji XMOVE

TOOL sensor_tool ; ustawienie TCP czujnika
  ;-----------------------------------------------------------
  ;           Dojazd do pozycji poszukiwania
  ;-----------------------------------------------------------
  HOME
  LMOVE start
  ;-----------------------------------------------------------
  ;           Przejazd przez oczekiwane pozycje stosu
  ;-----------------------------------------------------------
  ACCURACY 1 FINE
  SPEED pr_ruchu mm/s
  XMOVE p1 TILL 1001
  BREAK
  HERE found1
  SPEED pr_ruchu mm/s
  LMOVE p1
  SPEED pr_ruchu mm/s
  XMOVE p2 TILL 1001
  BREAK
  HERE found2
  SPEED pr_ruchu mm/s
  LMOVE p2
  SPEED pr_ruchu mm/s
  XMOVE p3 TILL 1001
  BREAK
  HERE found3
  SPEED pr_ruchu mm/s
  LMOVE p3
  MVWAIT 1
  LDEPART 100
  ;-----------------------------------------------------------
  ;           Obliczenie pozycji srodka okregu
  ;--------------------------------------------------------------------
  POINT cylinder_x = CCENTER (found1, found2, found3, start)

Przykład kodu z wykorzystaniem funkcji HSENSE

TOOL sensor_tool ; ustawienie TCP czujnika
  ;-----------------------------------------------------------
  ;           Dojazd do pozycji poszukiwania
  ;-----------------------------------------------------------
  SPEED 500 mm/s
  LmOVE start
  ;-----------------------------------------------------------
  ;           Aktywacja parametrow funkcji HSENSE
  ;-----------------------------------------------------------
  HSENSESET 1= 1001,20
  ;--------------------------------------------------------------------
  ;           Przejazd przez oczekiwane pozycje stosu
  ;-----------------------------------------------------------
  ACCURACY 1 FINE
  SPEED pr_ruchu mm/s ALWAYS
  LMOVE p1
  LMOVE p2
  LMOVE p3
  MVWAIT 1
  ;
  .num =0
  loop:
  HSENSE1 .result_var,sig_status[.num+1],#hsense_pos[.num+1],.err_var,.mem
  IF .err_var<>0 THEN
    .err = 3
    RETURN
  END
  ;
  IF .result_var == TRUE and sig_status[.num+1]== TRUE THEN
    POINT detect[.num+1] = #hsense_pos[.num+1]
    .num = .num+1
  END
  IF .mem GOTO loop
  ;
  HSENSESET 1 =0
  SPEED 500 mm/s
  LDEPART 100
  ;-----------------------------------------------------------
  ;           Obliczenie pozycji srodka okregu
  ;-----------------------------------------------------------
  POINT cylinder =CCENTER(detect[1],detect[2],detect[3],start)

Porównanie wyników

Kluczowymi parametrami do porównania obu rozwiązań są: czas działania programu oraz dokładność detekcji. W większości aplikacji zrobotyzowanych zależy nam na dwóch parametrach, precyzji i wydajności. Gdy mamy do dyspozycji sprzęt najwyżej jakości, taki jak roboty Kawasaki Robotics, warto wykorzystać pełnię jego potencjału dzięki sprytowi programisty i optymalnemu kodowi programu.

Przyjęto prędkości próbkowania dla ruchów poszukiwania jak w tabeli poniżej. Pozostałe ruchy wykonywane są z prędkością 500 mm/s.

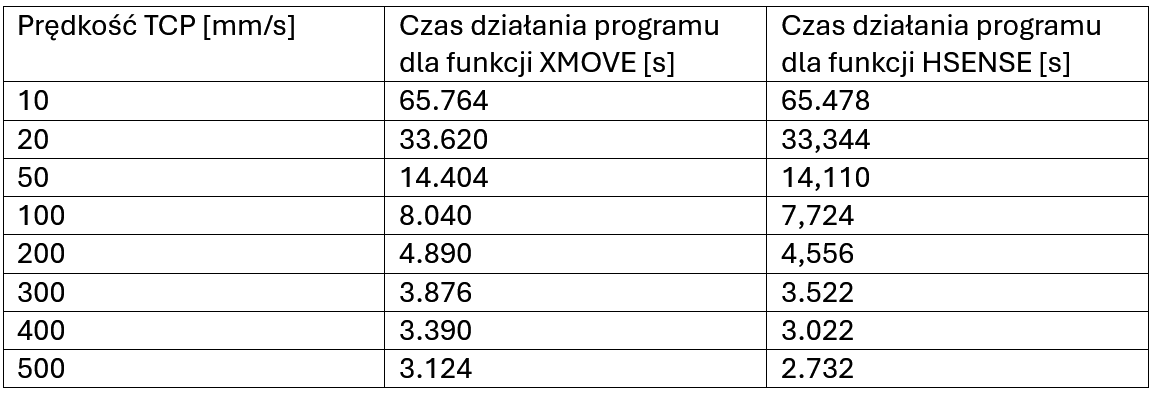
Porównanie uzyskanych dokładności w stosunku do pozycji w K-Roset:

Środek detalu w K-Roset został ustawiony na pozycji X 300, Y 600 względem układu bazowego robota .

Wykorzystując proste równanie na odległość punktu od środka okręgu jesteśmy w stanie sprawdzić, czy robot może bezkolizyjnie pobrać detal.

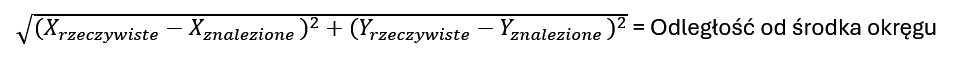
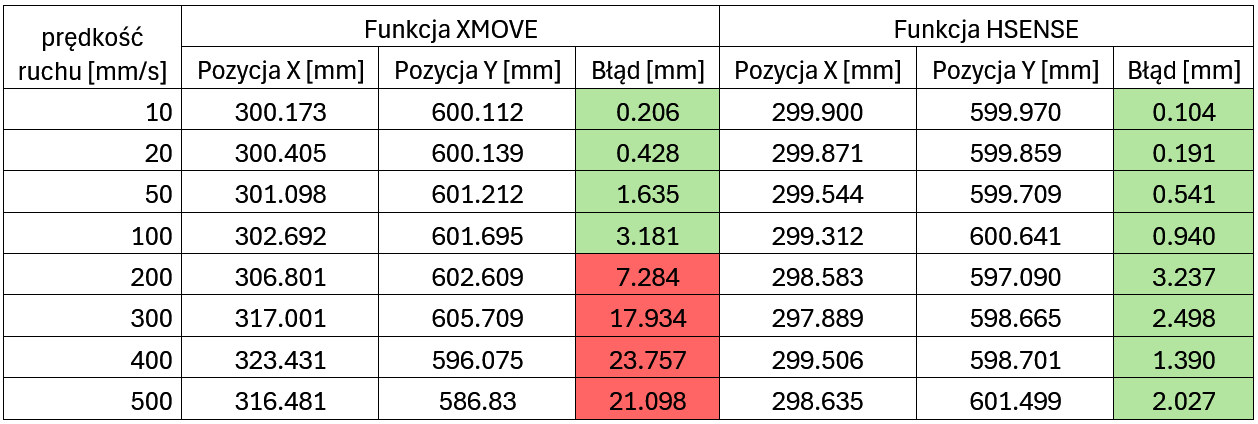
Na zielono zaznaczono wyniki prób, które spełniły nasze założenia bezkolizyjnej pracy.

Podsumowanie

Jak pokazały przedstawione testy, funkcja HSENSE dobrze sprawuje się w wykorzystaniu do pomiarów bezstykowych. Bufor 20 pozycji detekcji, możliwość reagowania na zbocza narastające i opadające, a także możliwość równoległego monitorowania dwóch sygnałów dają szerokie pole możliwości. W przypadku wykrywania obiektów, gdy nie istnieje ryzyko kolizji, znacząco może poprawić czas wyszukiwania, a zatem również czas cyklu całej aplikacji.

Funkcja XMOVE dobrze radzi sobie przy detekcji obiektów z niskimi prędkościami. Można ją wykorzystać do dokonywania pomiarów, jednak jest ona dedykowana do detekcji obiektów na ścieżce ruchu, tak aby w kolejnym kroku pobrać znaleziony przedmiot.

Jak pokazały wyniki testów, każda z funkcji może być użyta do detekcji obiektów. Jednak aby wykorzystać ich pełny potencjał, należy stosować je tam, gdzie pokażą swoją przewagę.

Funkcja HSENSE sprawdza się przy pomiarach bezstykowych, gdzie szybko możemy wyznaczyć punkty na krawędziach obiektu. Nie sprawdzi się natomiast w wypadku, gdy detekcja obiektu odbywa się na ścieżce kolizyjnej.

XMOVE pokaże swoją przewagę w detekcji i pobieraniu detalu znajdującego się na ścieżce kolizyjnej. Stosując dwa czujniki i kaskadę funkcji XMOVE możemy zbliżać się do np. stosu przekładek z wysoką prędkością. Po detekcji z bezpiecznej odległości przez pierwszy czujnik zwalniamy prędkość TCP robota i z niską prędkością poszukujemy dokładnej wysokości przekładki na stosie. Po jej detekcji zatrzymujemy robota i pobieramy przekładkę, a to wszystko na jednej ścieżce ruchu.

Stosując właściwą kombinację obu tych funkcji możemy uwolnić pełny potencjał wydajności i precyzji naszej aplikacji zrobotyzowanej.

Dodatek

Wyprowadzenie wzorów dla okręgu w przestrzeni trójwymiarowej.

Załóżmy punkty:

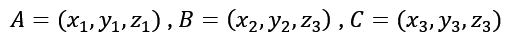
które znajdują się na okręgu, środek okręgu w punkcie S ma następujące współrzędne

1. Wyznaczamy wektory między punktami A,B,C:

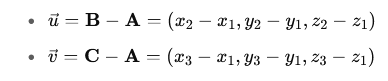
2. Wyznaczamy równanie płaszczyzny:

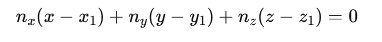
3. Wiedząc, że punkty na okręgu są równo oddalone o promień okręgu od środka okręgu:

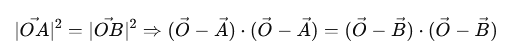
upraszczając wzór otrzymujemy:

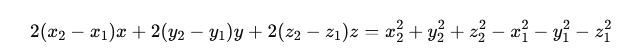
Podobnie dla punktów A i C możemy ułożyć równanie:

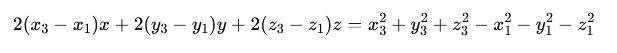
Trzecie równanie będzie wynikało z faktu, że punkt O leży na płaszczyźnie wyznaczonej przez punkty A,B,C:

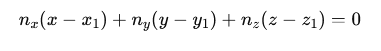
4. Układamy i rozwiązujemy układ trzech równań liniowych, wykorzystując metodę podstawienia dla uproszczenia zapisu.

Dla pierwszego równania  przyjęto:

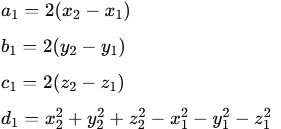
Analogicznie dla drugiego równania:

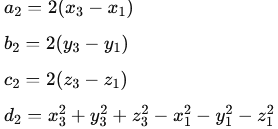
Oraz dla równania numer trzy:

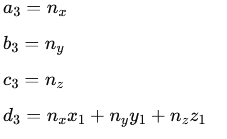
Uzyskując tym samym następujący układ równań:

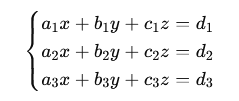
5. Korzystając z wzorów Cramera zapisujemy układ równań w postaci macierzowej i obliczamy wyznaczniki macierzy:

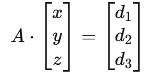
Macierz główna A ma następującą formę:

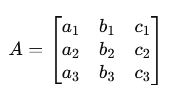
Na koniec obliczamy wyznaczniki macierzy:

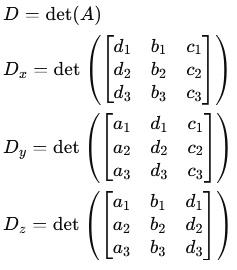
6. Po przekształceniach otrzymujemy współrzędne środka okręgu: